In [1,2] we introduced local input space histograms (LISHs) as a way to augment prototype-based, topology representing networks like the growing neural gas (GNG). LISHs help to capture more information about the underlying input space structure and improve the topology representation of the network, especially in cases of high-dimensional input data. However, regular GNGs lack an output representation that preserves the discovered neighborhood relations in such a way that the output can be used in subsequent stages of processing that rely on common distance measures. In [3] we show that the additional information provided by the LISHs can also be used to mitigate this problem. Based on the additional LISH information it is possible to form a sparse output representation that retains important neighborhood relations discovered by the GNG and makes this information accessible to common distance measures. We explore the properties of this sparse representation by a series of experiments in which we try to discover neighborhood relations in the MNIST database of handwritten digits [4] in an unsupervised fashion.
GNGs are a useful tool to discover and visualize structure in high-dimensional data. Another use case of prototype-based models like the GNG is vector quantization where the set of GNG units is used as a finite set of discrete entities to which the inputs are mapped. Typically, the output of this quantization for a particular input i is either the prototype of the respective closest unit or a one-hot encoded representation of the closest unit itself. The former output format can be used for tasks like reconstructing incomplete or noisy inputs, whereas the latter format is more suitable for, e.g., building histograms that describe the distribution of inputs. However, both output formats are not particularly useful in cases where the output of the GNG is used as input to a subsequent processing stage as neither output format preserves any neighborhood relations discovered by the GNG. Though it may be possible to construct a ranking of nearest prototypes according to a given distance measure when using the prototype-based output, such a ranking would be of limited value in the high-dimensional case as the actual similarity of the different entries is not described well by common distance measures like the Euclidean distance [2].


As a possible solution to this problem we propose a novel, relaxed one-hot encoding that represents not only a single unit of the GNG but also its direct neighborhood. In this representation the additional information provided by the local input space histograms is used to describe the direct neighborhood of a unit a in terms of the average bin error, i.e., the estimated input space density. If the input space between unit a and one of its neighbors b is dense, the corresponding entry in the output vector will be close to one. If the input space is sparse, the entry will be close to zero. As a consequence, output vectors of units that are direct neighbors or that share common neighbors will overlap in the corresponding entries allowing regular distance measures to detect these relationships. Using the LISH average bin error to quantify the strength of the neighborhood relations emphasizes those relations that are backed up by a continuum of input samples spanning the input space region between the particular units.
To investigate the proposed encoding we trained a GNG h with samples from the MNIST database and fed the output of h into a second GNG r using the relaxed one-hot encoding described above. Figure 1 shows the resulting structure of GNG r when both h and r have 50 GNG units. Subfigure 1a renders the prototypes of r as bitmaps with high values represented by light colors and low values represented by dark colors. The shown prototypes reveal the sparse patterns that result from the relaxed one-hot encoded input. As expected, neighboring units clearly exhibit similar sparse patterns corresponding to neighboring local regions in the original MNIST input space. To illustrate the latter relation figure 1b shows prototypes of GNG h superimposed on the network of GNG r. Each prototype was chosen according to the highest entry in the prototype vector of the respective unit in r. The overlay substantiates that neighboring units in the second GNG r do indeed refer to neighboring regions in the original MNIST input space of the underlying GNG h. Since both GNGs h and r have the same number of units, the second GNG r can allocate a single unit for each possible input pattern originating from h. As a consequence, the edges in r form mostly chains of units that refer pairwise to the most similar units in h with regard to the LISH average bin error between these units.
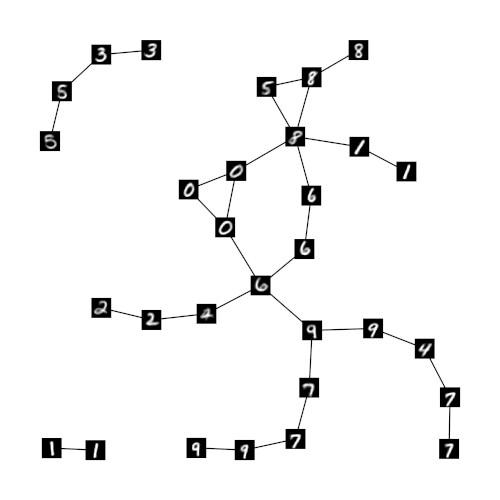
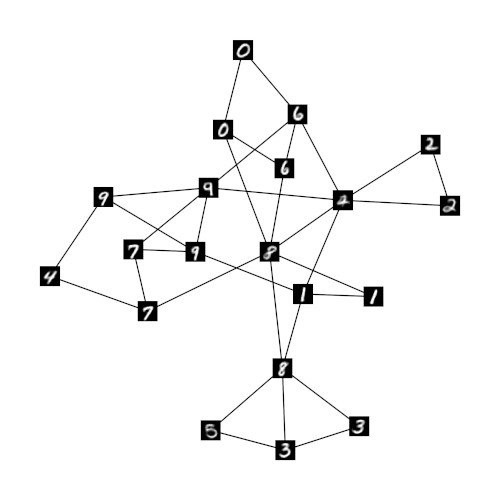
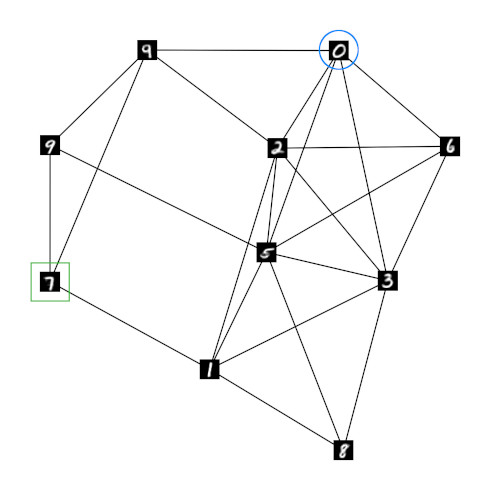
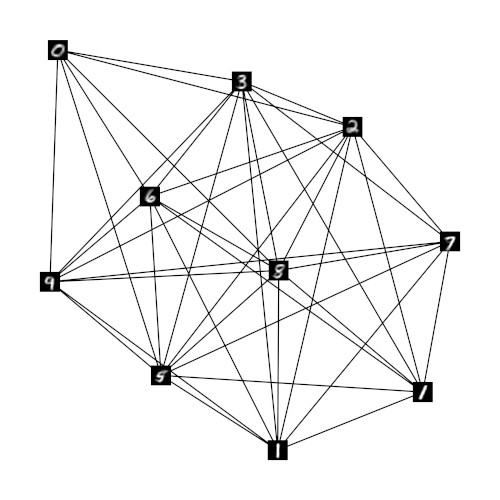
To show that the relaxed one-hot encoding can retain meaningful information on the relation of units in GNG h if the number of units in GNG r decreases we ran experiments with networks of size 30, 20, and 10. Figures 2a-c show these networks and their structure. As in figure 1b the shown prototypes originate from the underlying GNG h and are chosen according to the highest entry in the respective prototype vector of GNG r. The resulting network structures indicate that meaningful neighborhood relations can indeed be retained by the respective prototypes of the GNGs r . Even in the case of GNG r10 with only 10 units (fig. 2c) the average degree of the units remains low and the shown prototypes of neighboring units exhibit plausible similarities. In contrast, if the MNIST input space is processed directly by a GNG with only 10 units, the average degree per unit is significantly higher such that almost every unit has every other unit as direct neighbor (fig. 2d).


To provide a more detailed look at the composition of prototype vectors in GNG r10 figure 3 shows all vector entries with a value above 0.05 for two prototype vectors of r10, which are marked by a blue circle and a green square in figure 2c. In addition to their numerical value the shown entries are supplemented with renderings of the corresponding prototypes from the underlying GNG h. The entries are sorted left-to-right and top-to-bottom by value in descending order. The degree of similarity between the prototype associated with the highest value (top-left) and the remaining prototypes appears to correspond well to the numerical differences between the respective values. Furthermore, the number of prototype entries of substantial size is small compared to the overall number of entries (50), i.e., although the prototype vectors of GNG r10 refer to larger local regions in the underlying MNIST input space they remain sparse.
The ability to learn a single, meaningful sparse representation that covers multiple, similar input regions may prove to be an important property. Common prototype-based models represent their input space by a set of prototypes where each prototype represents a local region of input space. The shape of this local region depends on the used distance measure. In case of the widely used Euclidean distance each local region is a convex polyhedron. As a consequence, complex regions in the input space, e.g., a region that corresponds to a certain class of inputs (“number 0”, “flowers”, “faces”, etc.) have to be approximated piecewise by a group of prototypes. Identifying which prototypes belong to which group in an unsupervised fashion is a nontrivial task. The proposed relaxed one-hot encoding may facilitate this process by enabling the identification of neighboring prototypes through common distance measures. For example, the individual prototypes of the GNG r10 (fig. 2c) seem to capture at least some characteristics of the numerical classes, i.e., complex regions, that are present in the MNIST input space. Assuming that the resulting sparse representations of such a secondary model do represent classes or meaningful attributes, the sparseness of the representation may also be utilized to form combined representations, i.e., feature vectors that represent multiple attributes at once.
References
1
,
Supporting GNG-based clustering with local input space histograms,
In: Proceedings of the 22nd European Symposium on Artificial Neural Networks, Computational Intelligence and Machine Learning. Louvain-la-Neuve, Belgique, pp. 559–564, 2014,
[pdf|bibtex]
2
,
Analysis of high-dimensional data using local input space histograms,
In: Neurocomputing 169, pp. 272–280, 2015,
[pdf|doi|bibtex]
3
,
A Sparse Representation of High-Dimensional Input Spaces Based on an Augmented Growing Neural Gas,
In: GCAI 2016. 2nd Global Conference on Artificial Intelligence. Vol. 41. EPiC Series in Computing. EasyChair, pp. 303–313, 2016,
[pdf|doi|bibtex]
4
,
Gradient-based learning applied to document recognition,
In: Proceedings of the IEEE, 86, 2278-2324, 1998,
[doi]


