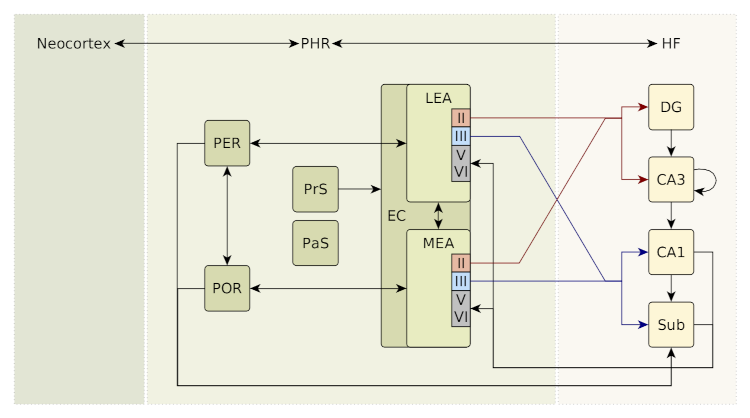
The parahippocampal region (PHR) and the hippocampal formation (HF) in the mammalian brain are vital for storing and retrieving episodic memories (Fig. 1), i.e., memories of specific events experienced by the organism [4,5,6]. A key requirement for this kind of memory is the ability to distinguish between similar events that may differ only in minute details. To accomplish such differentiation it is commonly assumed that parts of the hippocampus carry out some form of pattern separation that orthogonalizes the input signals before they are stored in an autoassociative memory [7,8,6]. As a result of this pattern separation, similar input signals cause divergent sets of neurons to become active and thus reduce confusion of these inputs in subsequent processing steps. Within the hippocampus such divergent activation of neurons in response to similar inputs was primarily observed in the dentate gyrus (DG) [7,9]. However, how this observed pattern separation in the DG arises is not well understood [6].
In [1] we offer a novel hypothesis regarding this problem. We show that the input space encoding produced by the RGNG grid cell model leads to a strong pattern separation that already occurs within the entorhinal cortex (EC) itself. As the latter provides the main input to the DG [3] we hypothesize that the pattern separation observed in DG is facilitated by output signals from the EC that are already well separated and that the DG itself just improves this separation by sparsification. In contrast to previous grid cell experiments the well-known MNIST database of handwritten digits [10] (Fig. 2a) is used as input signal to the RGNG model. To measure the degree of pattern separation the intra-class and inter-class cosine similarity distributions occuring in the MNIST dataset (Fig. 2b) are compared with the corresponding distributions occuring in the ensemble activity of the RGNG-modeled neuron group (Fig. 2c). A cosine similarity between two pattern with a value close to 1 indicates high similarity between the patterns; a value close to 0 indicates a high degree of dissimilarity (i.e., the vectors are orthogonal). Using the MNIST dataset allows for a more intuitive interpretation of the results as it is straightforward to judge the general similarity of digits. For example, the distribution of the intra-class cosine similarities for the digit “1” (Fig. 2b) is skewed towards the value 1 as there is less variation in how people write a “1” vs., e.g., a “5”. Also, all inter-class distributions are generally skewed towards the value 0 as digits are usually more similar to themselves as to other digits.
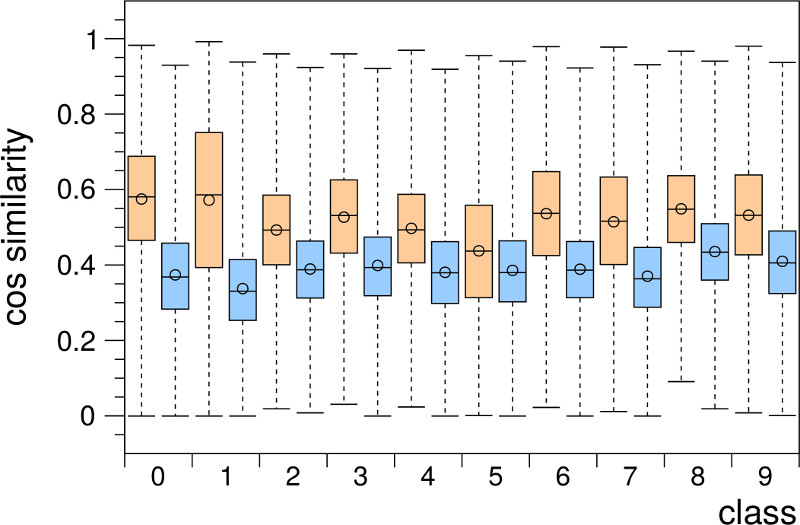
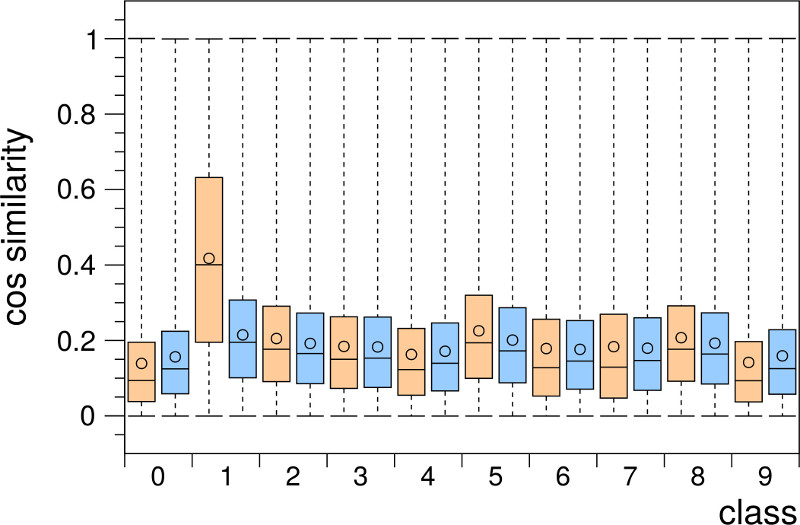
Figure 2c shows one example of a typical set of cosine similarity distributions occurring in the ensemble activity vectors of a simulated grid cell group that learned an encoding of the MNIST input space. The distributions are consistently closer towards the value 0 indicating an improved pattern separation. Furthermore, the difference between intra- and inter-class distributions is much less pronounced (except in digit class “1”). This orthogonalization of inputs can be further improved by combining the outputs of multiple grid cell groups that represent the input space in different resolutions or represent different parts of the input space [1].
Using the MNIST database as an input space has the added benefit that one can interpret the dendritic prototypes learned by individual cells more easily. Figure 3 shows the prototypes learned by three cells. Each cell learned a representation of the entire space by representing each digit class multiple times. As the prototypes differ between cells, each cell will react to a given input with a different degree of activity resulting in an ensemble activity of the entire neuron group that is like a fingerprint or signature for the given input.
In summary, the results presented in [1] indicate that entorhinal grid cells may indeed perform pattern separation on their input signals and thus may provide already orthogonalized output signals to the hippocampus. These results challenge established views on the parahippocampal-hippocampal region and provide a novel explanation for the origin of the pattern separation that is observed in the dentate gyrus.



References
1
,
Entorhinal Grid Cells May Facilitate Pattern Separation in the Hippocampus,
In: Proceedings of the 9th International Joint Conference on Computational Intelligence, IJCCI 2017, Funchal, Madeira, Portugal, November 1-3, pp. 141–148, 2017,
[pdf|doi|bibtex]
2
,
A Computational Model of Grid Cells based on a Recursive Growing Neural Gas,
In: PhD thesis. University of Hagen, 2016,
[pdf|bibtex]
3
,
The anatomy of memory: an interactive overview of the parahippocampal-hippocampal network,
In: Nat Rev Neurosci, 10(4):272–282, 2009,
[doi]
4
,
Episodic and declarative memory: Role of the hippocampus,
In: Hippocampus, 8(3):198–204, 1998,
[doi]
5
,
The Human Hippocampus and Spatial and Episodic Memory,
In: Neuron, 35(4):625 – 641, 2002,
[doi]
6
,
The mechanisms for pattern completion and pattern separation in the hippocampus,
In: Frontiers in Systems Neuroscience, 7(74), 2013,
[doi]
7
,
Pattern Separation in the Dentate Gyrus and CA3 of the Hippocampus,
In: Science, 315(5814):961–966, 2007,
[doi]
8
,
Pattern separation in the hippocampus,
In: Trends in neurosciences, 34(10):515–525, 2011,
[doi]
9
,
Strong Evidence for Pattern Separation in Human Dentate Gyrus,
In: Journal of Neuroscience, 36(29):7569–7579, 2016,
[doi]
10
,
Gradient-based learning applied to document recognition,
In: Proceedings of the IEEE, 86, 2278-2324, 1998,
[doi]


