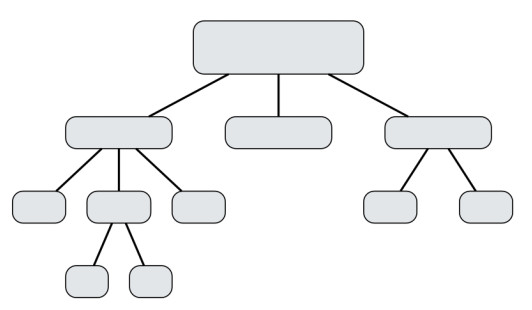
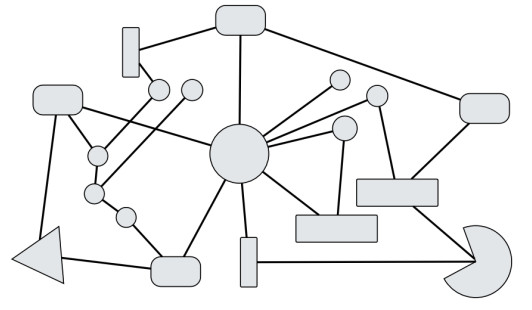
The analysis, modeling and simulation of complex systems is generally acknowledged as a hard problem. The main argument in this regard is based upon the distinction between complicated and complex systems. While both types of systems can consist of many interacting constituents, the former type has a fully known and well-formed structure, e.g., in the form of a hierarchy (Fig. 1a), whereas the latter type is characterized as a collection of heterogeneous, highly interconnected constituents that lack such a structure (Fig. 1b) and thus – according to common reasoning – can not be analyzed with otherwise successful and widespread reductionistic methods. Although this argument hints at the right direction as to why it is difficult to analyze complex systems, the conclusion drawn appears premature. The sole fact that a complex system consists of heterogeneous, highly interconnected entities does not suffice to make this system hard to analyze. According to the given description a complex system would be nothing more than some form of complicated graph – a structure for which a rich set of tools exists in computer science and mathematics.

(a)

(b)

In a complex system it is likely that the relations between its constituents change considerably over time. In contrast to complicated systems, where such changes occur only rarely or not at all, it is an important and distinctive feature of complex systems. A good example for this kind of change can be observed in neural networks where the relations between different neurons change constantly in response to the activation of the involved neurons. In Artificial Neural Networks these changing relations between neurons are commonly modeled as weighted connections whose weights vary in course of a particular learning process. As the actual weights of the connections are only determined during runtime based on the input data, it is impossible to predict the connection weights in advance, i.e., during design-time, and thus it is not possible to exactly specifiy which neuron will contribute to which output of the system. As a consequence, it is very difficult among other things to determine how many neurons arranged in which configuration are sufficient to produce the desired behavior of the network. A slightly different kind of changing relations between constituents of a complex system can be described by Agent-based models. In this case the relations between the constituents, i.e. agents, are induced by a shared environment. As the agents move, their relations, e.g. their relative positions to each other, change over time. In contrast to Artificial Neural Networks the relations between the constituents of an Agent-based model are not explicitly modeled. Instead, they are implicitly defined by the particular environment of the model. On the one hand this implicit definition of relations enables the intuitiv modeling of a complex system by translating the perceived structure of the system almost one to one into the structure of the Agent-based model. On the other hand this approach may obfuscate important relations which should be stated explicitly in order to isolate and precisely characterize them.

These examples illustrate that it is not the sheer amount of connections between the entities of a complex system which cause the system to be difficult to analyze and model. It is the fact, that those connections are only potential connections that can vary over time.

The second characteristic of complex systems regarding the difficulty of analyzing and modeling is more subtle and it relates to the way we humans perceive and think. Our main mental strategy to cope with arbitrarily complex matters is the use of categorisation. Typically we begin by taking (perceived) continua and breaking them down into manageable categories. For example, if we want to address the wavelength emitted by an object we see, we break the continuous visible spectrum of wavelengths down into a small number of categories, i.e. colors. When matters get more complex, we aggregate categories into more abstract super-categories. As this process continues we build up ever more abstract categories. If such a higher-level category is contemplated, the constituting lower-level sub-categories become increasingly less present in working memory, thus effectively hiding the full complexity of the higher-level category and keeping the perceived complexity approximately constant. This strategy enables us to think about arbitrarily complex matters without the need to actually address the full complexity of the particular matter at once.

In fact, even if we would want to address the full complexity of some matter at once, we would not be able to do so. As soon as we start to explore some aspect of a higher-level category by recursively breaking down the category into its lower-level sub-categories we are bound to a limited number of items that we can store in our working memory at once. Thus, while dealing with some specific detail of a higher-order category we temporarily lose sight of the ”big picture”. When dealing with complicated systems like the one depicted in figure 1a, this limitation poses no serious problem to the analysis and modeling since the different sub-parts of a complicated system are cleanly separated from each other. For each sub-part of the system it is sufficient to define a proper interface that hides the internal structure and allows for ”black boxing” the particular sub-part.

In contrast, when dealing with complex systems the approach of piece by piece analysis and modeling of the system is not without problems as the assumption of cleanly separated sub-parts is usually not true for a complex system. As a result, the previously decribed strategy of ”black boxing” which corresponds well to the way we mentally deal with complex matters does not fit the structure of complex systems. Instead, the categories involved in complex systems frequently share common sub-categories that give rise to potentially unanticipated, mutual influences. These potential side-effects can be difficult to notice and track since the involved sub-categories may not be readily present in the working memory of the person that is performing the analysis. As described before, our mental strategy for dealing with complex matters hides the full complexity of higher-level categories by keeping the lower-level sub-categories out of working memory. Hence, lower-level sub-categories that are shared between different parts of the complex system can easily be overlooked.

(a)

(b)

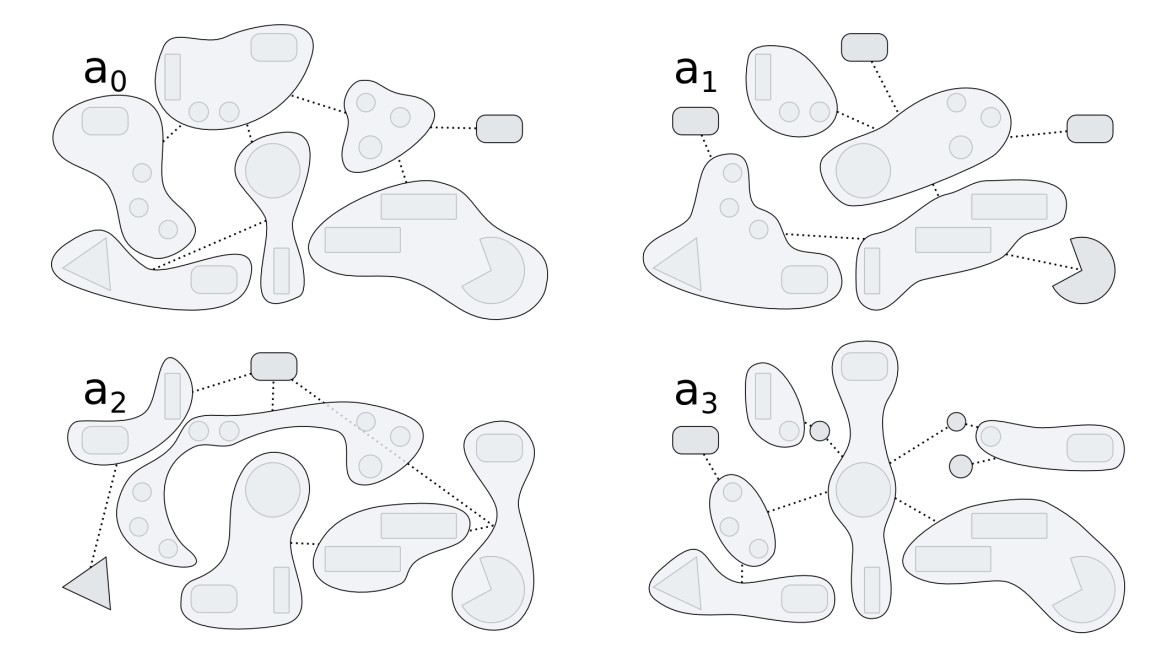
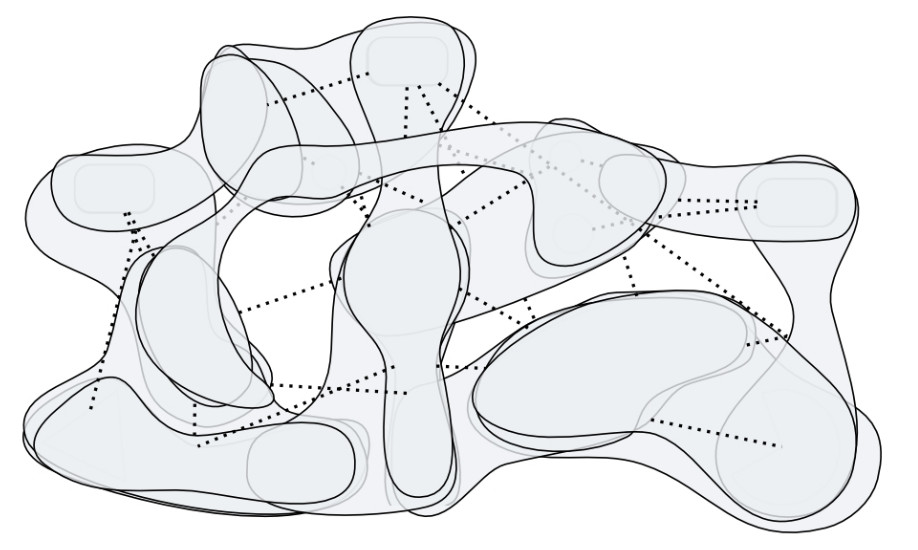
Furthermore, the intricate relations of higher- and lower-level categories attributed to a complex system affect the constituents of the corresponding model since the constituents are predominantly deduced from these categories. As a result, constituents of the model that reflect certain aspects of the complex system inherit some of the intricate relations from the underlying categories, i.e. they overlap to a certain extent where the underlying categories share common lower-level subcategories. Figure 2 illustrates this by showing the constituents of a hypothetical complex system with respect to four different aspects (Fig. 2a) and their resulting superposition when the constituents corresponding to the different aspects are merged into a single model of the complex system (Fig. 2b). The mutual influences of shared lower-level categories hint at potential side-effects between overlapping constituents that have to be considered in order to model the paricular complex system correctly.

The foregoing considerations as to why complex systems are difficult to analyze and model can be summarized as follows:

• The relations between the constituents of a complex system can vary over time in non-trivial ways and thus cannot be specified in advance. The particular computational model which is being used has to provide structures and mechanisms that allow for a determination of these relations at runtime.
• Mutual influences between constituents of a complex system are not only represented by higher-level categories as in complicated systems but are also indicated by shared, lower-level categories. As the mental analysis of a complex matter typically progresses from higher-level categories towards lower-level categories while simultaneously only a limited number of items can be kept in working memory at once, it is difficult to reliably identify the mutual influences occurring between the constituents of a complex system.
• If a complex system is analyzed with respect to different aspects, the resulting constituents for each aspect can ”conceptually overlap” when they are merged into a single model of the system. These overlaps hint at potential side-effects between the involved constituents and suggest that a further fragmentation of the corresponding constituents may be necessary in order to transform the implicit side effects into explicit relations.

Existing computational models for complex systems focus predominantly on the first point by providing structures and mechanisms to deal with dynamic relations between constituents. The main aspect involving the latter two points, i.e. the granularity and identification of suitable constituents, is usually not handled explicitly. Instead, it is implicitly predefined by the characteristics of the specific variation of complex systems that is favored by the particular model. In order to treat this aspect explicitly, I present a generalized computational model for complex systems in [1,2] that addresses these issues.

References

 1  Jochen Kerdels and Gabriele Peters,
A generalized computational model for modeling and simulation of complex systems,
In: Research Report 4. University of Hagen, 2012,
[pdf|bibtex]

 2  Jochen Kerdels and Gabriele Peters,
Exploratory Modeling of Complex Information Processing Systems,
In: ICINCO (1), pp. 514–521, 2013,
[pdf|bibtex]